Quantum Zeta Epiphany

Numbers like π, e and φ often turn up in unexpected places in science and mathematics. Pascal’s triangle and the Fibonacci sequence also seem inexplicably widespread in nature. Then there’s the Riemann zeta function, a deceptively straightforward function that has perplexed mathematicians since the 19th century. The most famous quandary, the Riemann hypothesis, is perhaps the greatest unsolved question in mathematics, with the Clay Mathematics Institute offering a $1 million prize for a correct proof.
UC Santa Barbara physicist Grant Remmen believes he has a new approach for exploring the quirks of the zeta function. He has found an analogue that translates many of the function’s important properties into quantum field theory. This means that researchers can now leverage the tools from this field of physics to investigate the enigmatic and oddly ubiquitous zeta function. His work could even lead to a proof of the Riemann hypothesis. Remmen lays out his approach in the journal Physical Review Letters.
“The Riemann zeta function is this famous and mysterious mathematical function that comes up in number theory all over the place,” said Remmen, a postdoctoral scholar at UCSB’s Kavli Institute for Theoretical Physics. “It’s been studied for over 150 years.”
An outside perspective
Remmen generally doesn’t work on cracking the biggest questions in mathematics. He’s usually preoccupied chipping away at the biggest questions in physics. As the fundamental physics fellow at UC Santa Barbara, he normally devotes his attention to topics like particle physics, quantum gravity, string theory and black holes. “In modern high-energy theory, the physics of the largest scales and smallest scales both hold the deepest mysteries,” he remarked.
One of his specialties is quantum field theory, which he describes as a “triumph of 20th century physics.” Most people have heard of quantum mechanics (subatomic particles, uncertainty, etc.) and special relativity (time dilation, E=mc2, and so forth). “But with quantum field theory, physicists figured out how to combine special relativity and quantum mechanics into a description of how particles moving at or near the speed of light behave,” he explained.
Quantum field theory is not exactly a single theory. It’s more like a collection of tools that scientists can use to describe any set of particle interactions.
Remmen realized one of the concepts therein shares many characteristics with the Riemann zeta function. It’s called a scattering amplitude, and it encodes the quantum mechanical probability that particles will interact with each other. He was intrigued.
Scattering amplitudes often work well with momenta that are complex numbers. These numbers consist of a real part and an imaginary part — a multiple of √-1, which mathematicians call i. Scattering amplitudes have nice properties in the complex plane. For one, they’re analytic (can be expressed as a series) around every point except a select set of poles, which all lie along a line.
“That seemed similar to what’s going on with the Riemann zeta function‘s zeros, which all seem to lie on a line,” said Remmen. “And so I thought about how to determine whether this apparent similarity was something real.”
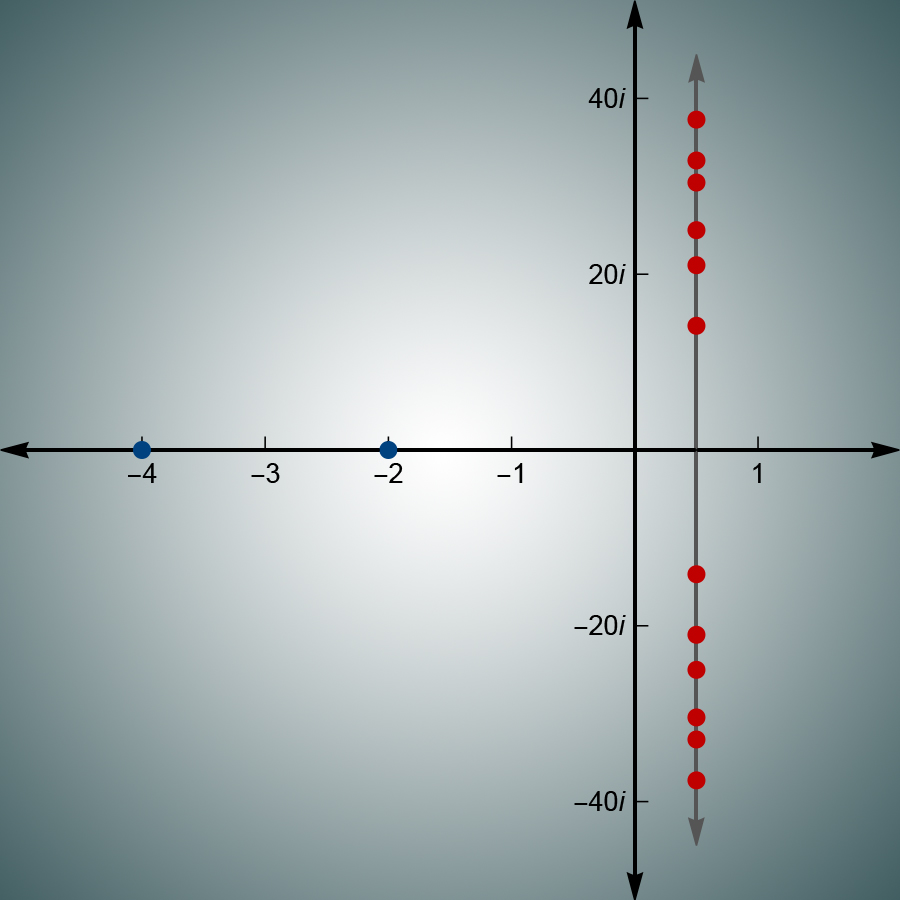
The zeta function maps all the colored points to zero. The non-trivial zeros (red) all seem to lie on a line where the real component of the number equals ½.
Photo Credit: GRANT REMMEN, HARRISON TASOFF
The scattering amplitude poles correspond to particle production, where a physical event happens that generates a particle with a momentum. The value of each pole corresponds with the mass of the particle that’s created. So it was a matter of finding a function that behaves like a scattering amplitude and whose poles correspond to the non-trivial zeros of the zeta function.
With pen, paper and a computer to check his results, Remmen set to work devising a function that had all the relevant properties. “I had had the idea of connecting the Riemann zeta function to amplitudes in the back of my mind for a couple years,” he said. “Once I set out to find such a function, it took me about a week to construct it, and fully exploring its properties and writing the paper took a couple months.”
Deceptively simple
At its core, the zeta function generalizes the harmonic series:
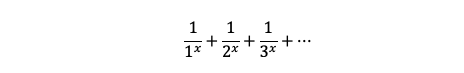
This series blows up to infinity when x ≤ 1, but it converges to an actual number for every x > 1.
In 1859 Bernhard Riemann decided to consider what would happen when x is a complex number. The function, now bearing the name Riemann zeta, takes in one complex number and spits out another.
Riemann also decided to extend the zeta function to numbers where the real component was not greater than 1 by defining it in two parts: the familiar definition holds in places where the function behaves, and another, implicit definition covers the places where it would normally blow up to infinity.
Thanks to a theorem in complex analysis, mathematicians know there is only one formulation for this new area that smoothly preserves the properties of the original function. Unfortunately, no one has been able to represent it in a form with finitely many terms, which is part of the mystery surrounding this function.
Given the function’s simplicity, it should have some nice features. “And yet, those properties end up being fiendishly complicated to understand,” Remmen said. For example, take the inputs where the function equals zero. All the negative even numbers are mapped to zero, though this is apparent — or “trivial” as mathematicians say — when the zeta function is written in certain forms. What has perplexed mathematicians is that all of the other, non-trivial zeros appear to lie along a line: Each of them has a real component of ½.
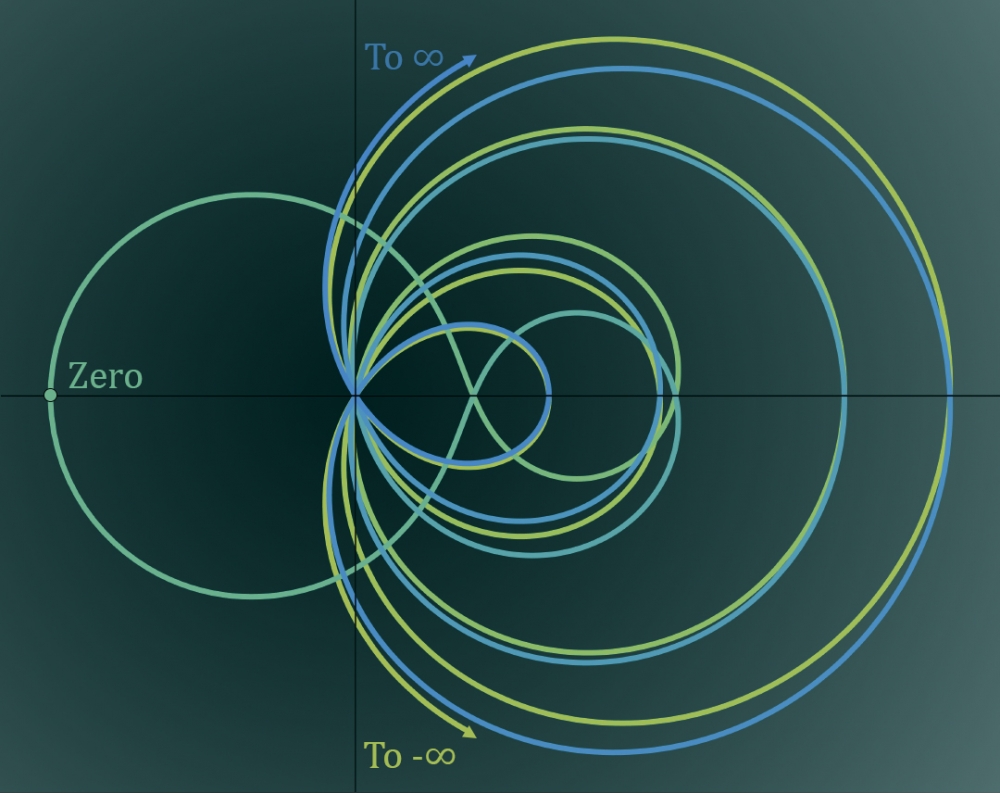
The zeta function transforms the grey line from the previous image into this curve. Each of the red points is a spot where this curve passes through the origin (0,0).
Photo Credit: GRANT REMMEN, HARRISON TASOFF
Riemann hypothesized that this pattern holds for all of these non-trivial zeros, and the trend has been confirmed for the first few trillion of them. That said, there are conjectures that work for trillions of examples and then fail at extremely large numbers. So mathematicians can’t be certain the hypothesis is true until it’s proven.
But if it is true, the Riemann hypothesis has far-reaching implications. “For various reasons it crops up all over the place in fundamental questions in mathematics,” Remmen said. Postulates in fields as distinct as computation theory, abstract algebra and number theory hinge on the hypothesis holding true. For instance, proving it would provide an accurate account of the distribution of prime numbers.
A physical analogue
The scattering amplitude that Remmen found describes two massless particles interacting by exchanging an infinite set of massive particles, one at a time. The function has a pole — a point where it cannot be expressed as a series — corresponding to the mass of each intermediate particle. Together, the infinite poles line up with the non-trivial zeros of the Riemann zeta function.
What Remmen constructed is the leading component of the interaction. There are infinitely more that each account for smaller and smaller aspects of the interaction, describing processes involving the exchange of multiple massive particles at once. These “loop-level amplitudes” would be the subject of future work.
The Riemann hypothesis posits that the zeta function’s non-trivial zeros all have a real component of ½. Translating this into Remmen’s model: All of the amplitude’s poles are real numbers. This means that if someone can prove that his function describes a consistent quantum field theory — namely, one where masses are real numbers, not imaginary — then the Riemann hypothesis will be proven.
This formulation brings the Riemann hypothesis into yet another field of science and mathematics, one with powerful tools to offer mathematicians. “Not only is there this relation to the Riemann hypothesis, but there’s a whole list of other attributes of the Riemann zeta function that correspond to something physical in the scattering amplitude,” Remmen said. For instance, he has already discovered unintuitive mathematical identities related to the zeta function using methods from physics.
Remmen’s work follows a tradition of researchers looking to physics to shed light on mathematical quandaries. For instance, physicist Gabriele Veneziano asked a similar question in 1968: whether the Euler beta function could be interpreted as a scattering amplitude. “Indeed it can,” Remmen remarked, “and the amplitude that Veneziano constructed was one of the first string theory amplitudes.”
Remmen hopes to leverage this amplitude to learn more about the zeta function. “The fact that there are all these analogues means that there’s something going on here,” he said.
And the approach sets up a path to possibly proving the centuries-old hypothesis. “The innovations necessary to prove that this amplitude does come from a legitimate quantum field theory would, automatically, give you the tools that you need to fully understand the zeta function,” Remmen said. “And it would probably give you more as well.”



